Zk-SNARKs in Substrate (Part 1)
In this article I would like to introduce you to the zk-SNARKs (zero-knowledge succinct non-interactive argument of knowledge) concept. First we are going to briefly describe what are the zero-knowledge proofs, what are the stages of creating them, which tools can be useful for generating the zk-SNARKs. Also, we will touch a little math behind them. I encourage you to visit our GitHub, where you can find a repository for this article. Let’s start with the definition of the zero-knowledge proof and then we will move to the zk-SNARKs.

Zero-knowledge proof is a method where one party (the prover) tries to “convince” the other party (the verifier) that a given statement is true, without revealing the solution ^6. There are two types of proving systems^2:
- interactive - where the prover and verifier exchange multiple messages with each other, until the verifier is convinced enough that the prover knows the given statement is true.
- non-interactive - where the prover creates a proof and the verifier is able to run it and check if the given statement is true. Compared to the interactive version, there is only one message (proof) that is sent to the verifier and it can be run asynchronously.
In this article we will focus on the non-interactive approach which is called zk-SNARKs (zero-knowledge succinct non-interactive argument of knowledge).
zk-SNARKs
From the high-level point of view, the concept defines:
- public inputs that are known to everyone. - private inputs that are only known for the prover. He claims that these are the right inputs for solving the problem. - Problem - a function
, which takes private and public inputs. Result of this function is boolean: or . - Prover - he knows the solution for the problem (private inputs), based on that he can create a proof.
- Verifier - he can accept a proof and verify it.
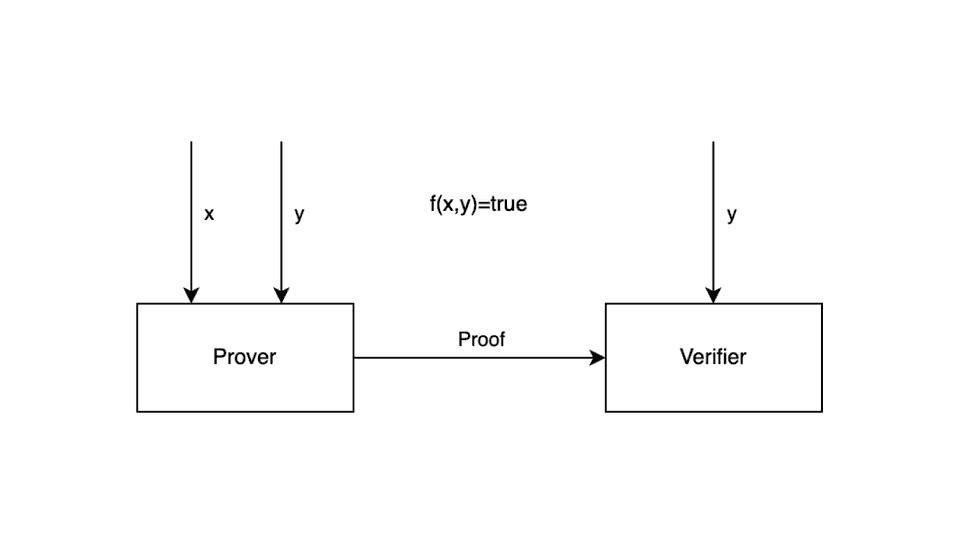
As shown on the image, the prover will create a proof, based on the public and private inputs. Verifier will receive it and run the verification knowing only the public inputs. Based on that we can conclude that proof will need somehow to wrap our problem and the private inputs. Then it will need to transform them to the other form which could be verified only with the public inputs. Now when we know the concept, we can dive deeper and look at this process in detail.
First let’s think about the problems which zk-SNARKs can solve. There are two types of problems P(deterministic polynomial) and NP (nondeterministic polynomial)^5. The first ones are the problems that can be run in polynomial time and those are not applicable for the zk-SNARKs^4. The second ones are the problems, which can only be verified in polynomial time. In other words, finding the right solution for an NP problem is very hard, but verifying an already existing one is quite easy. This is exactly what zk-SNARKs is about.
First, our problem will need to be written as a code and then transformed into the proper form, which is a Quadratic Arithmetic Program (QAP)^1. Transformation allows us to convert code into a mathematical representation of it. In the next parts of this article, we take a closer look at this process.
If we want to go further, we will need to have a suitable example, which helps us in better understanding the concept of zk-SNARKs. Let’s assume that Bob is a founder of the Bright Coders union. In front of his mates, he announces that there are few places left in the union and those who solve this equation first:
will be able to join it! Alice is one of his friends who knows the result, which is
If we take a closer look at the equation and set it together with what we already knew about the zk-Snarks, we will notice two things:
- Equation is well know to everyone, so result “12” can be our “public input”
- “x” is what we are looking for, so this can be our “private input”. This matches the requirement for only a prover (Alice) to know its value.
Now together with Alice we will try to explain the process of converting the equation above into the zk-SNARK. The process takes a couple of stages:
- Computation statement
- Flattening
- R1CS (Rank-1 Constraint System)
- QAP (Quadratic Arithmetic Program)
We are going to describe them in the next part of this article. Alice is going to use two external tools Cricom and SnarkJS. Circom is a compiler written in Rust for creating circuits. SnarkJS is a npm package, which implements generation and validation of the zk-SNAKRs for the artifacts produced by Circom. For the installation process, please check our documentation in the repository.
Computation statement
Alice will start with writing our equation as a Rust function
fn solution(x: i32) -> i32 {
let y = x*x + 3;
return y;
}
by using it, she can easily verify if value "3" is the right answer for our equation. At this stage, it is good to point out that Alice could build a binary and send it to Bob asking him to verify the result. Unfortunately we have two problems here:
- Alice will need to reveal the value of the “x” variable to Bob, which she doesn’t want to.
- Bob will not be sure if Alice's program is the correct one. For example her program could just return “12”, without doing any computations.
Solving those problems can be done by converting this program to QAP and adding some cryptography. This is what we are going to do next steps.
Flattening
We need to convert our computation statement to a few smaller ones which have one of two forms^1:
- Assignment to the variable or constants (
, where “y” be a variable or a constant) - Assignment to the combination of operators (
, where “*op” is one of the and “y” and “z” can be variables or constants).
You can think about those statements as gates of an arithmetic circuit. The result of the flattening for our statement will be:
fn solution(x: i32) -> i32 {
let tmp1 = x*x;
let y = tmp1 + 3;
return y;
}
Rank-1 Constraint System
Next step is to convert our circuits to a R1CS (rank-1 constraint system), which is a list of three vectors
where:
- “
” is a dot product in and is a number of circuits
We can interpret this in this way, if our vectors could represent the constraints (equation which describes circuits), then vector
We will start with the definition of
Now when we defined the witness we can conclude the vectors for the
first circuit
second circuit
If we put everything together for the first circuit, we can check the correctness of the R1CS equation:
| 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 12 |
| 1 | 1 | 0 | 3 |
| 0 | 0 | 1 | 9 |
As you can see the computations are fine, so R1CS for circuit one is ok. Alice will now use a Cricom for generating a R1CS. First she need to creates a Cricom template file (task.cricom) which defines a constraints for our code:
pragma circom 2.0.0;
template Task() {
signal input x;
signal output y;
signal tmp_1;
tmp_1 <== x * x;
y <== tmp_1 + 3;
}
component main = Task();
Than she can generate R1CS by running the command:
mkdir build
circom task.circom --r1cs --wasm --sym -o build --O0 -p bls12381
This will generate a file (build/task.r1cs), which describes an R1CS in the Cricom. Another artifact is a build/task.wasm, which is a circuit compiled to the WebAssembly. After that Alice will need to create a witness (vector
{"x": "3"}
Then she can generate a witness file (build/witness.wtns):
cd build/task_js
node generate_witness.js task.wasm ../../input.json witness.wtns
Alice can also verify the result, by exporting witness to json (build/witness.json):
snarkjs wtns export json witness.wtns witness.json
[
"1",
"12",
"3",
"9"
]
As you can see, the result is exactly the same as it were for our witness from the computations.
Quadratic Arithmetic Program
The last step is to convert a R1CS to QAP, which will allow us to transform R1CS vectors to the polynomials. The logic behind the equation will still be the same, but instead of using vectors with a dot product we will use polynomials^3. We can start with the declaration of the polynomials
Based on those points, we can create polynomials by using a Lagrange interpolation. As a result we will get a set of polynomials which can be then written in the equation:
where:
Why can we write this equality here? As you remember we are now in the scope of the polynomials, so we can define a polynomial
From the polynomial long division, we can deduce that above equation will only hold, if
Ok, so we get the definition of
Alice knows the witness and she’s able to compute
Summary
At this point we are going to stop. What we already learned is what the zk-SNARKs are and how we can use tools like Circom and SnarkJS in creating them. In the next post, we will take a closer look at the Groth16, which is a cryptography proof system that will allow us to finish the Alice task. We will use artifacts (witness.wtns, input.json) created in this tutorial, to generate a proof and verify it using SnarkJS.
Read Part 2 of Zk-Snarks in the Substrate Tutorial.
This tutorial is supported by the Web3 Foundation Grants Program.
